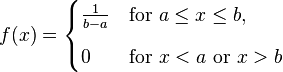| Comments

Various Distributions With Incanter

I was looking for ways to get random numbers from various distributions in Clojure.
Here’s how I got it with Incanter.

Below are the list of distributions mentioned in this page.

Through out this page, I used below project.clj.

Uniform distribution

Probability density function(PDF) of Uniform Distribution:


(From http://en.wikipedia.org/wiki/Uniform_distribution_(continuous))

This is pretty straight forward.

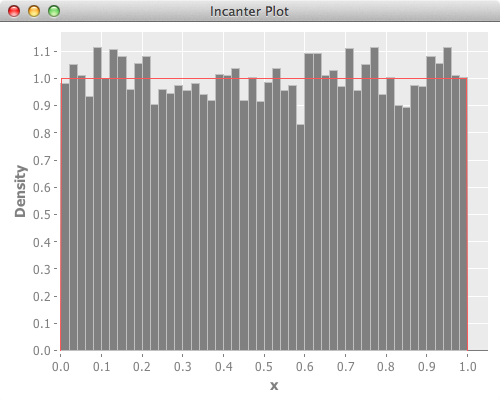
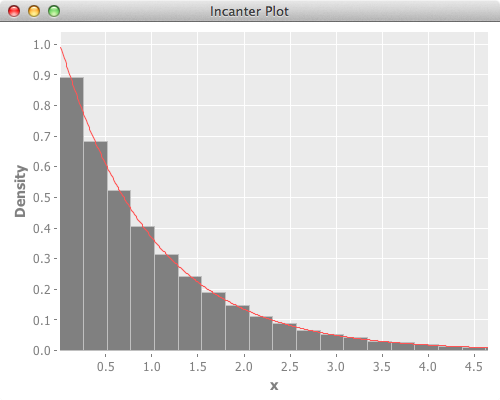
Here’s the plot. Red line is theoretical value.

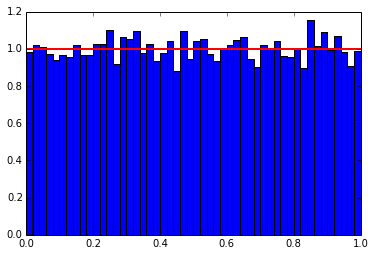
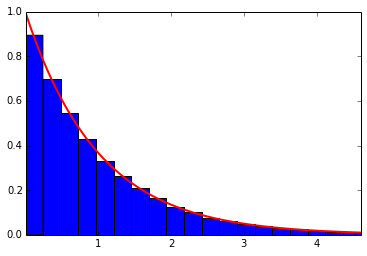
Below is the reference scipy version, and it’s plot.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

import numpy as np
from scipy.stats import uniform
import matplotlib.pyplot as plt

np.random.seed()
N = 10000
rv = uniform(loc=0.0, scale=1.0)
x = rv.rvs(size=N)
nbins = 50
plt.hist(x, nbins, normed=True)

x = np.linspace(rv.ppf(0), rv.ppf(1), 100)
plt.plot(x, uniform.pdf(x), 'r-', lw=2, label='uniform pdf')

plt.show()

Exponential distribution

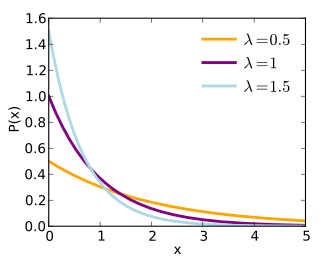
PDF of Exponential Distribution:


(From http://en.wikipedia.org/wiki/Exponential_distribution)

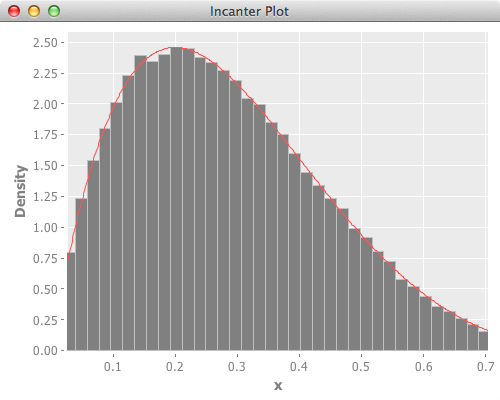
Since incanter didn’t have ppf(Percent point function, inverse of cdf), I used percentile of the created random values to get lower and upper range for drawing plot.

"incanter exponential plot"

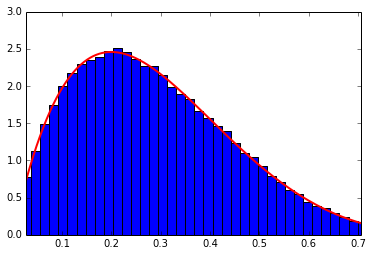
Below is the reference scipy version, and it’s plot.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

import numpy as np
from scipy.stats import expon
import matplotlib.pyplot as plt

np.random.seed()
N = 100000
rv = expon(scale=1.0)
x = rv.rvs(size=N)
nbins = 50
plt.hist(x, nbins, normed=True)

x = np.linspace(rv.ppf(0.01), rv.ppf(0.99), 1000)
plt.plot(x, rv.pdf(x), 'r-', lw=2, label='uniform pdf')
plt.xlim((rv.ppf(0.01), rv.ppf(0.99)))

plt.show()

"scipy exponential plot"

Beta distribution



(From http://en.wikipedia.org/wiki/Beta_distribution)

"incanter beta distribution(a=2, b=5)"

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

import numpy as np
from scipy.stats import beta
import matplotlib.pyplot as plt

np.random.seed()
N = 100000
rv = beta(a=2.0, b=5.0)
x = rv.rvs(size=N)
nbins = 50
plt.hist(x, nbins, normed=True)

x = np.linspace(rv.ppf(0.01), rv.ppf(0.99), 1000)
plt.plot(x, rv.pdf(x), 'r-', lw=2, label='uniform pdf')
plt.xlim((rv.ppf(0.01), rv.ppf(0.99)))

plt.show()

"scipy beta plot(a=2, b=5)"

References

Helpful references were:

Comments