| Comments

In the last post, I explored how to get below disributions with incanter.

Incanter supports various distributions: (From: http://incanter.github.io/incanter/distributions-api.html)

  • beta-distribution
  • binomial-distribution
  • chisq-distribution
  • exponential-distribution
  • f-distribution
  • gamma-distribution
  • integer-distribution
  • neg-binomial-distribution
  • normal-distribution
  • poisson-distribution
  • t-distribution
  • uniform-distribution

But Scipy stats supports lot more distributions.
In JVM world, there’s another library that supports various distributions called Apache Commons Math, and here are list of distributions supported by the library. In order to make those distributions available from Incanter world, I’ve created small library called incanter-contrib-distribution.

Below are some of the examples of how to use it.

Cauchy distribution

PDF of Cauchy distribution:


(From http://en.wikipedia.org/wiki/Cauchy_distribution)

Cauthy distribution has wide support, so for plotting, filtered out values out of certain range.

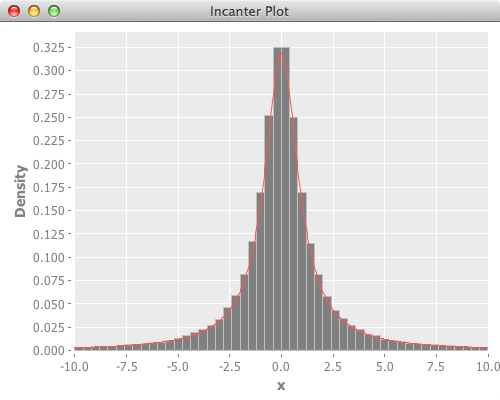
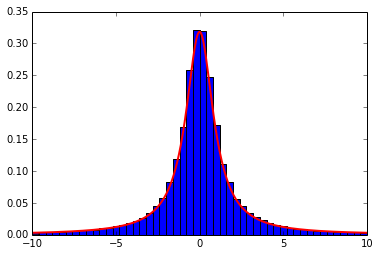
Below is the reference scipy version, and it’s plot.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

import numpy as np
from scipy.stats import cauchy
import matplotlib.pyplot as plt

np.random.seed()
N = 100000
rv = cauchy(loc=0.0, scale=1.0)
x = rv.rvs(size=N)
x = x[(x>-10) & (x<10)]
nbins = 50
plt.hist(x, nbins, normed=True)

x = np.linspace(-10, 10, 1000)
plt.plot(x, rv.pdf(x), 'r-', lw=2, label='cauchy pdf')
plt.xlim((-10, 10))

plt.show()

"scipy cauchy distribution plot"

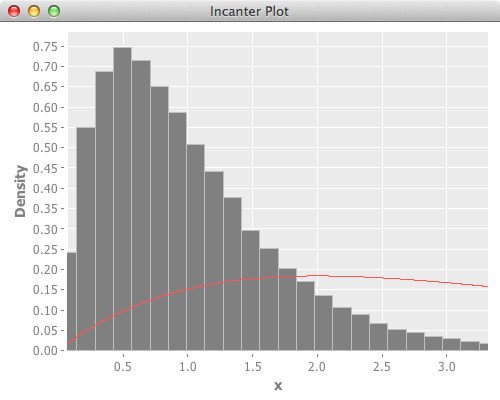
Gamma distribution

PDF of Gamma Distribution:


(From http://en.wikipedia.org/wiki/Gamma_distribution)

Gamma distribution exists in incanter, but in incanter-1.5.5, there’s still issue around draw.
Here’s how it’s not properly working with incanter-1.5.5 gamma-distribution.

Though this was fixed in issue#245 and is available in head, I used incanter-contrib-distributions for this for now.

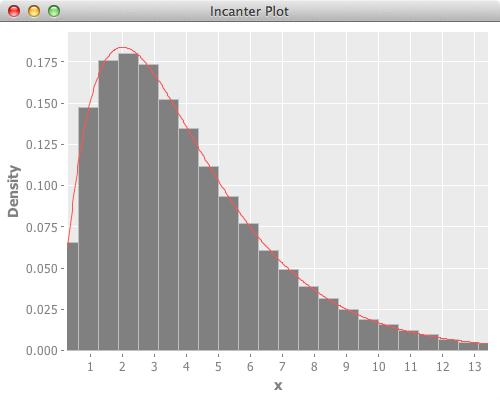
Below is the reference scipy version, and it’s plot.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

import numpy as np
from scipy.stats import gamma
import matplotlib.pyplot as plt

np.random.seed()
N = 100000
rv = gamma(a=2.0, scale=2.0)
x = rv.rvs(size=N)
nbins = 50
plt.hist(x, nbins, normed=True)

x = np.linspace(rv.ppf(0.01), rv.ppf(0.99), 1000)
plt.plot(x, rv.pdf(x), 'r-', lw=2, label='uniform pdf')
plt.xlim((rv.ppf(0.01), rv.ppf(0.99)))

plt.show()

"scipy gamma plot k=2, theta=2"

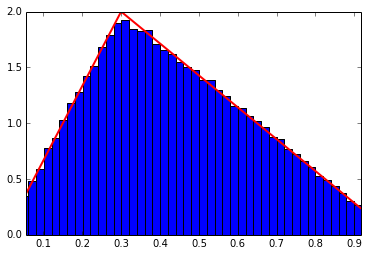
Triangular Distribution

PDF of Triangular Distribution:


(From http://en.wikipedia.org/wiki/Triangular_distribution

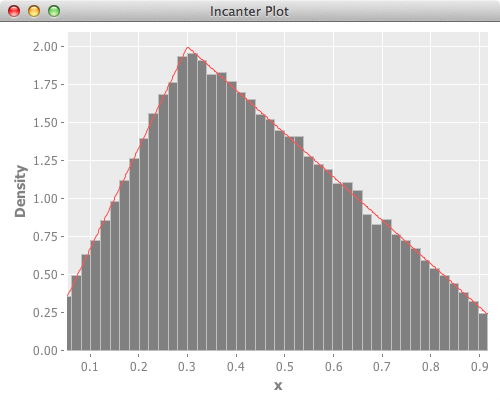
Below is the reference scipy version, and it’s plot.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

import numpy as np
from scipy.stats import triang
import matplotlib.pyplot as plt

np.random.seed()
N = 100000
rv = triang(loc=0.0, c=0.3, scale=1.0)
x = rv.rvs(size=N)
nbins = 50
plt.hist(x, nbins, normed=True)

x = np.linspace(rv.ppf(0.01), rv.ppf(0.99), 1000)
plt.plot(x, rv.pdf(x), 'r-', lw=2, label='triang pdf')
plt.xlim((rv.ppf(0.01), rv.ppf(0.99)))

plt.show()

| Comments

I was looking for ways to get random numbers from various distributions in Clojure.
Here’s how I got it with Incanter.

Below are the list of distributions mentioned in this page.

Through out this page, I used below project.clj.

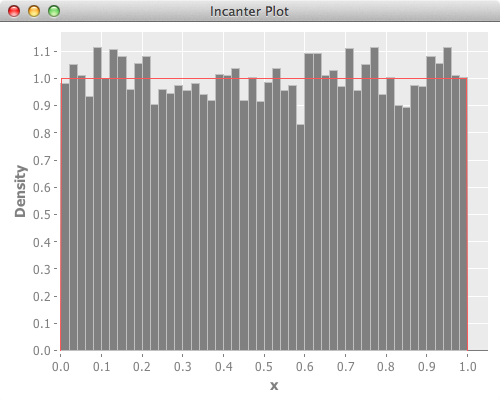
Uniform distribution

Probability density function(PDF) of Uniform Distribution:


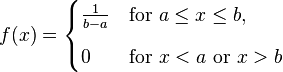
(From http://en.wikipedia.org/wiki/Uniform_distribution_(continuous))

This is pretty straight forward.

Here’s the plot. Red line is theoretical value.

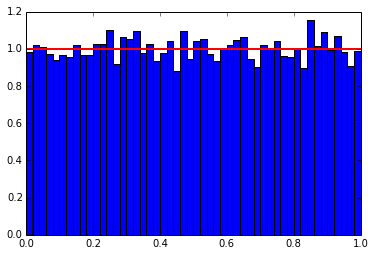
Below is the reference scipy version, and it’s plot.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

import numpy as np
from scipy.stats import uniform
import matplotlib.pyplot as plt

np.random.seed()
N = 10000
rv = uniform(loc=0.0, scale=1.0)
x = rv.rvs(size=N)
nbins = 50
plt.hist(x, nbins, normed=True)

x = np.linspace(rv.ppf(0), rv.ppf(1), 100)
plt.plot(x, uniform.pdf(x), 'r-', lw=2, label='uniform pdf')

plt.show()

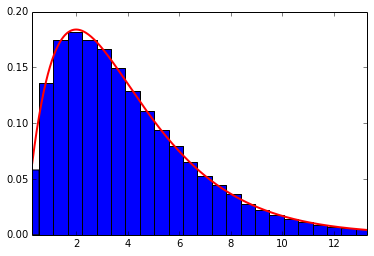
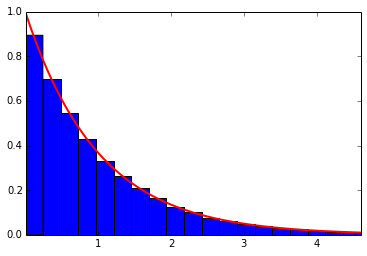
Exponential distribution

PDF of Exponential Distribution:


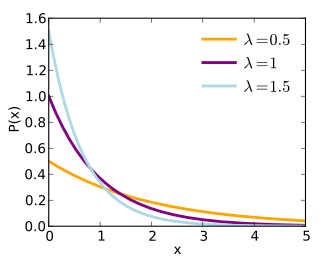
(From http://en.wikipedia.org/wiki/Exponential_distribution)

Since incanter didn’t have ppf(Percent point function, inverse of cdf), I used percentile of the created random values to get lower and upper range for drawing plot.

"incanter exponential plot"

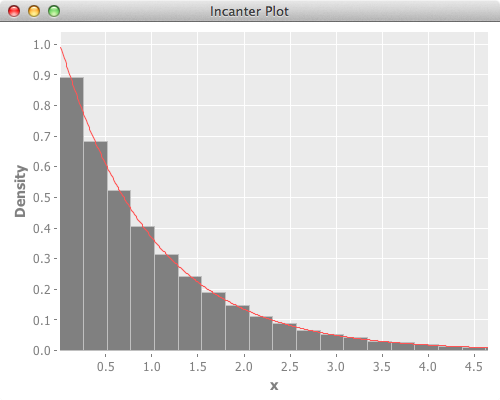
Below is the reference scipy version, and it’s plot.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

import numpy as np
from scipy.stats import expon
import matplotlib.pyplot as plt

np.random.seed()
N = 100000
rv = expon(scale=1.0)
x = rv.rvs(size=N)
nbins = 50
plt.hist(x, nbins, normed=True)

x = np.linspace(rv.ppf(0.01), rv.ppf(0.99), 1000)
plt.plot(x, rv.pdf(x), 'r-', lw=2, label='uniform pdf')
plt.xlim((rv.ppf(0.01), rv.ppf(0.99)))

plt.show()

"scipy exponential plot"

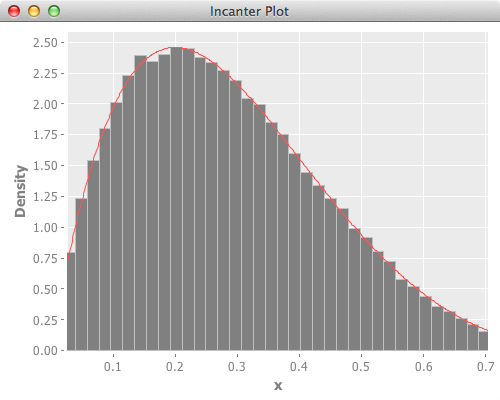
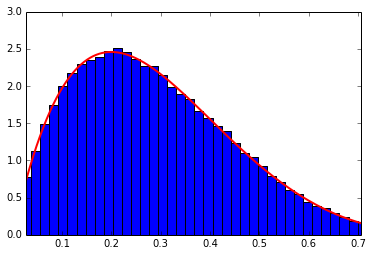
Beta distribution



(From http://en.wikipedia.org/wiki/Beta_distribution)

"incanter beta distribution(a=2, b=5)"

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

import numpy as np
from scipy.stats import beta
import matplotlib.pyplot as plt

np.random.seed()
N = 100000
rv = beta(a=2.0, b=5.0)
x = rv.rvs(size=N)
nbins = 50
plt.hist(x, nbins, normed=True)

x = np.linspace(rv.ppf(0.01), rv.ppf(0.99), 1000)
plt.plot(x, rv.pdf(x), 'r-', lw=2, label='uniform pdf')
plt.xlim((rv.ppf(0.01), rv.ppf(0.99)))

plt.show()

"scipy beta plot(a=2, b=5)"

References

Helpful references were:

| Comments

Started blog page using octopress.
Followed instructions on this page, and here.

While installing octopress, I encountered below error:

1

 ! [rejected]        master -> master (non-fast-forward)

I was able to get this fixed by following this in stackoverflow.